La course
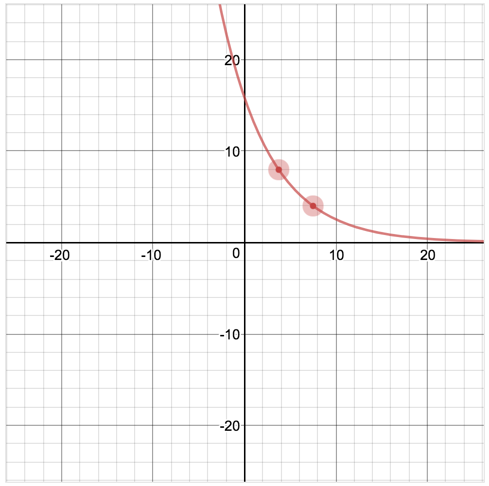
Dans cette activité, les élèves utilisent le raisonnement proportionnel pour prédire combien de temps il faudra à quelqu’un pour courir sept milles. Les élèves étudieront également la signification de plusieurs éléments graphiques dans leur contexte.
Traduction: Jocelyn Dagenais