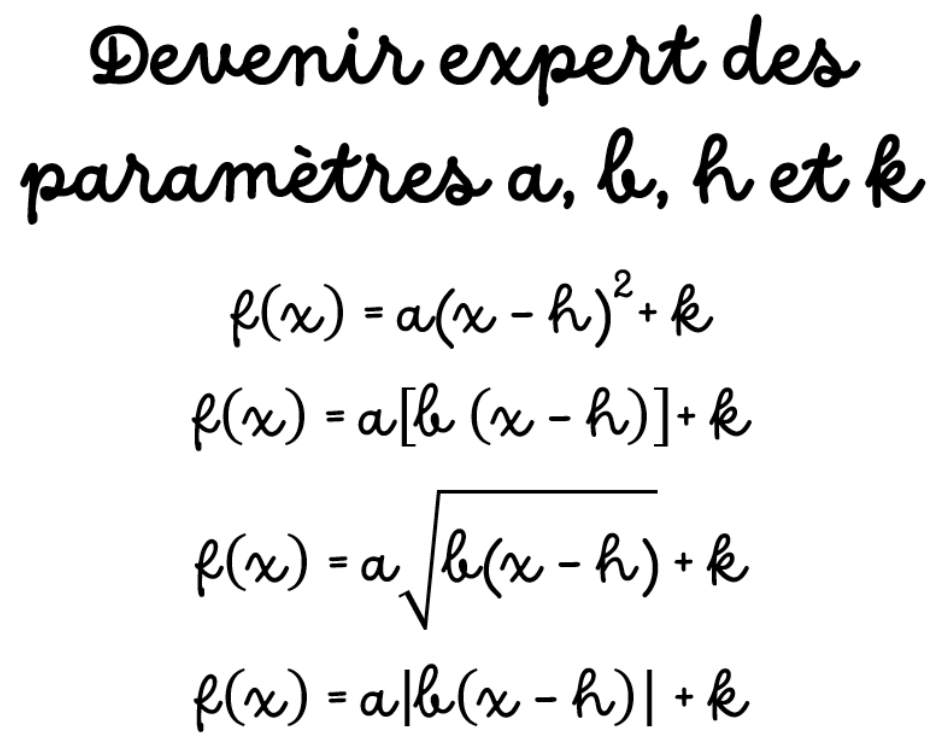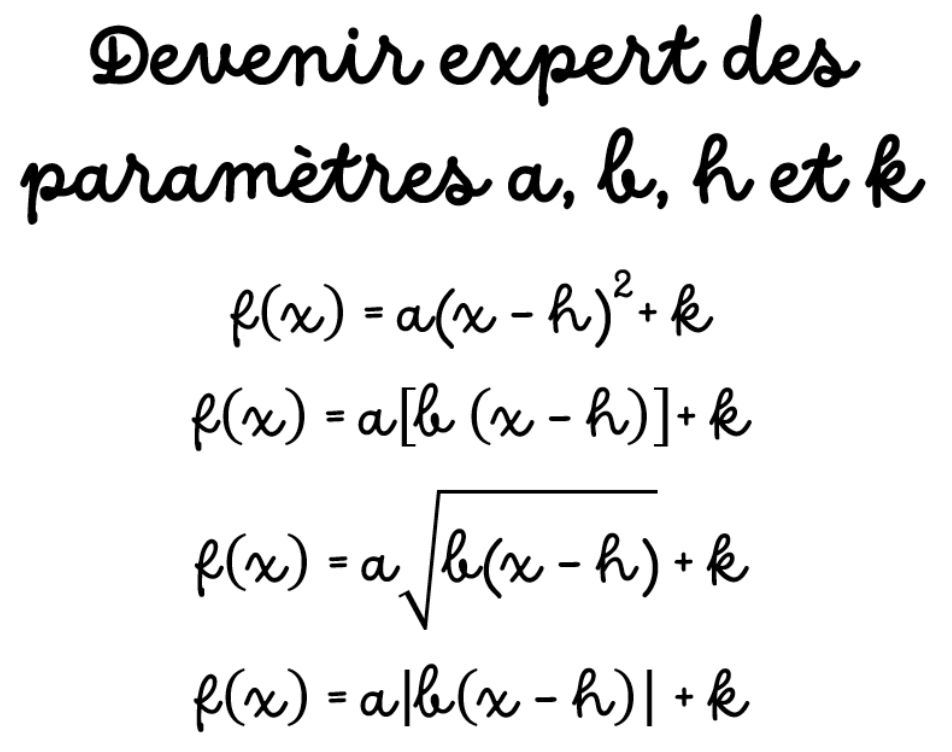SN5 Paramètres a, b, h et k partie 2
À la fin de cette activité, tu devras être capable, sans calculatrice ni Desmos, de trouver l’équation canonique d’une fonction à partir de son graphique et ce, pour quatre fonctions:
– fonction quadratique
– fonction partie entière
– fonction racine carrée
– fonction valeur absolue