Activités francophones utilisant Desmos Classroom et Polypad
Activités francophones utilisant Desmos Classroom et Polypad
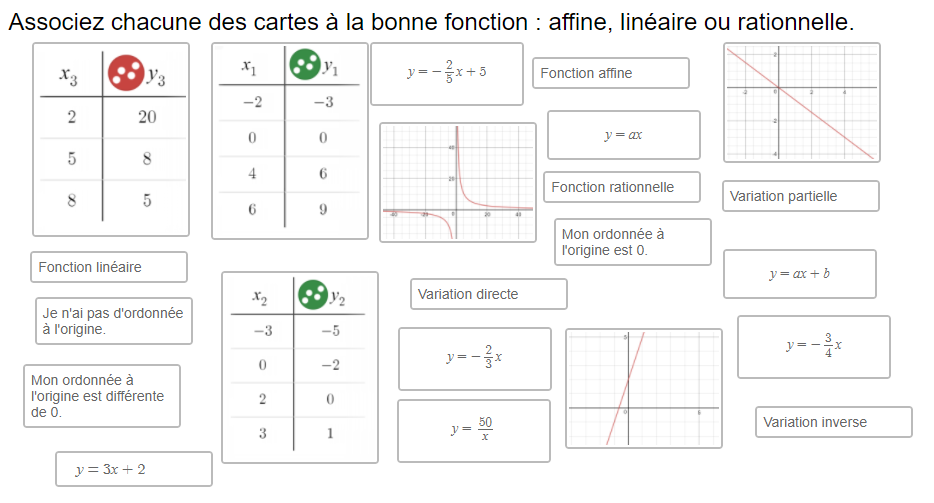
Dans cette activité d’association, les élèves travaillent les différentes représentation d’expression algébrique (représentation verbale, table de valeur, représentation visuelle et représentation algébrique).
Après le card sort, il est possible d’avoir une discussion sur les notions d’équivalence et de commutativité.
Traduction: Julie Cléroux
Ce polygraphe est conçu pour susciter des conversations riches sur les histogrammes. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: allure, centre, étendue, symétrie, incliner à droite, incliner à gauche, moyenne, médiane, extremums.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des histogrammes de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser une langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Julie Cléroux
Dans cette activité, les élèves doivent écrire des équations linéaires pour modéliser le parcours d’une balle de golf. Cette activité suppose que les élèves ont de l’expérience dans la représentation graphique d’équations linéaires.
Astuce du pro: Pour les élèves qui ont du mal à démarrer sur un trou en particulier, invitez-les à tracer un point quelque part entre la balle et le trou à utiliser comme «cible» lors de la création du premier segment de droite.
Note: Les trous 6-7 ont été créés par Christopher Kunkel. Voir l’article du blog pour plus de détails: http://whenmathhappens.com/2014/04/11/putt-putt-golf/
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves utilisent un modèle pour prédire le coût d’une pizza extra-large, basé sur des informations à propos de la taille et le coût de deux petites pizzas. Les élèves choisissent entre un modèle linéaire, quadratique ou exponentiel, ou construisent le leur avec une fonction différente s’ils le souhaitent. Les élèves interpréteront également les paramètres de leur équation en contexte.
Crédit d’image: écrans 1-4, papajohns.com
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves explorent l’idée d’ «inclinaison» de segments de droite. Cette activité sert de prélude à des conversations formelles sur le déplacement vertical, le déplacement horizontal et la pente.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves compareront les pentes des droites avec une ordonnée à l’origine de zéro. Ils utiliseront leurs comparaisons pour apprendre à écrire les équations des droites de la forme y = ax.
Inspiré par l’étude du taux de variation d’une équation de Caleb Rothe:
https://teacher.desmos.com/activitybuilder/custom/5673095054bf1351078e195d#
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les nombres rationnels et irrationnels. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: positif, négatif, fraction, rationnel et irrationnel.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Les élèves utiliseront les taux unitaires de diverses façons pour comparer la sucrosité de cinq céréales. Ils classent les céréales des moins aux plus sucrées et interprètent des graphiques pour déterminer les informations utiles, en particulier le taux unitaire.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves mettent en relation les notions apprises sur les fonctions du premier degré et la fonction rationnelle en 3e secondaire FGA.
Vocabulaire, règles, tables de valeurs, graphiques.
Utilisez un modèle rectangulaire basé sur l’aire et la distributivité pour construire la compréhension conceptuelle de la multiplication des polynômes (en particulier les binômes).
Prévoyez d’utiliser cette activité sur plusieurs jours si nécessaire.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves doivent décrire le domaine et l’image dans six relations. Par la suite, les élèves utilisent des points mobiles pour créer trois fonctions avec des critères spécifiques pour le domaine et l’image.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves pourront entrer leurs données afin de trouver combien d’élastiques seront nécessaires pour effectuer le saut de bungee par Barbie.
Dans cette activité, les élèves pratiquent comment trouver l’équation d’une droite afin d’atterrir l’avion sur la piste. La plupart des défis sont bien adaptés pour la forme pente-ordonnée à l’origine, mais selon les objectifs de certains élèves ou de certaines classes, les équations peuvent facilement être modifiées.
Inspiré par Hit the Runway by Danny Whittaker: https://teacher.desmos.com/activitybuilder/custom/56274598fc26d37312cf969b
Traduction: Litissia Abi Abdallah et Jocelyn Dagenais
Avec les paramètres m et b d’une fonction de variation partielle, l’élève explore leur rôle graphiquement. Diverses activités sont déployées afin de l’aider à comprendre ce rôle dans le graphique.
Une série de 4 conjectures reliées à l’équation des droites. Niveau de difficulté varié.
Cette activité introduit les probabilités aux élèves avec des roues de la chance. Quel résultat est plus probable, rouge ou bleu ? Les élèves répondent à cette question en recueillant et en analysant les données de la classe, puis en appliquant ce qu’ils ont appris pour évaluer la probabilité d’autres expériences aléatoires.
Traduction: Jocelyn Dagenais
Une idée d’activité qu’il est possible de faire en classe avec la corde à linge mathématique, à l’aide de Desmos ou à l’aide d’une vraie corde à linge mathématiques.
Permet de travailler la compréhension d’expressions algébriques en 2e secondaire ou encore les inéquations en 3e secondaire.
Pour avoir accès à la construction du graphique et le modifier: https://www.desmos.com/calculator/bzy2ybtp9r
Dans cette activité, les élèves explorent les relations entre l’aire et la mesure des côtés des carrés comme porte d’entrée au nombre rationnels et irrationnels.
Pendant l’activité, les élèves en apprendront plus sur:
– les carrés parfaits et les racines carrées
– les nombres rationnels et irrationnels
– placer approximativement un nombre rationnel et irrationnel sur la droite numérique
* Note à l’enseignant: Attention à l’écran 5 pour approfondir la conversation sur les nombres rationnels.
**Cartes Clothesline ici: http://bit.ly/squaredancecards
***Billet de blogue sur les idées pédagogiques ici: http://burnsmath.blogspot.com/2017/05/a-visual-representation-of-square-roots.html
Traduction: Jocelyn Dagenais (originalement d’Andrew Stadel)
Activité portant sur la notion de moyenne pondéré, mais sans utiliser le calcul.
Association de cartes afin de travailler les lois des exposants
L’équation de la droite en troisième secondaire.
Traduction d’une activité d’Andrew Stadel.
Les élèves auront besoin d’utiliser un langage moins informel et un langage plus formel pour décrire les relations linéaires.
Un élève tentera de «décrire» (sans utiliser ses mains) un graphique que son partenaire doit dessiner (qui ne peut pas parler). Ensuite, les deux échangeront de rôle.
Après quelques défis, votre classe aura utilisé un certain nombre de mots pour décrire les relations linéaires. Maintenant vous pouvez échanger ces mots informels pour ceux plus formels.
Traduction d’une activité de Jon Orr: https://teacher.desmos.com/activitybuilder/custom/59b93f81e6dafd05ab6ba30d
Jouer au billard avec les droites, en utilisant « Marbleslides »
Voici une série de défis proposés par les élèves du groupe CST414-01 de l’école secondaire Chanoine-Beaudet !
Amusez-vous!
Pour télécharger la feuille de consignes remise aux élèves:
https://drive.google.com/file/d/0B7ac4YpzuCpZY3FlTEE3MFVmSkk/view?usp=sharing
Dans cette activité, les élèves écrivent des équations linéaires sous la forme y = mx + b pour comparer le coût des t-shirts de deux compagnies. Les élèves tirent ensuite des conclusions entre la représentation algébrique et graphique des solutions, et interprètent les résultats en contexte.
Traduction: Jocelyn Dagenais