Activités francophones utilisant Desmos Classroom et Polypad
Activités francophones utilisant Desmos Classroom et Polypad
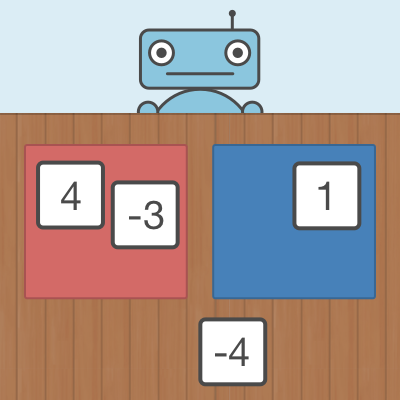
Dans cette activité, les élèves additionnent des entiers dans le contexte d’un jeu de cartes. Le but du jeu est de créer deux groupes de cartes, chacune avec la même somme. Celui qui utilise le plus de cartes gagne!
Traduction: Jocelyn Dagenais
Ce Polygraph personnalisé est conçu pour susciter des conversations riches en vocabulaire sur des figures géométriques, y compris des polygones et un cercle. Le vocabulaire clé qui peut apparaître dans les questions des élèves comprend: côté, sommet / sommets, angle, scalène, régulier, isocèle, équilatéral, aigu, droit, obtus, parallèle, isométriques, congrus, opposé, triangle, quadrilatère, carré, rectangle, parallélogramme, trapèze, cerf-volant, pentagone, hexagone et cercle.
Dans les premiers tours du jeu, les élèves peuvent remarquer des formes de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégie, mettre en évidence des questions efficaces et encourager les élèves à utiliser un langage académique de plus en plus précis. Selon leur niveau de compréhension atteint, vous pourriez encourager vos élèves à utiliser le système de grille pour déterminer la longueur / la pente des segments de droite afin de vérifier les affirmations concernant les côtés isométriques, parallèles et / ou perpendiculaires. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage précis au travail.
Traduction: Jocelyn Dagenais
Dans cette activité d’association, les élèves travaillent les différentes représentation d’expression algébrique (représentation verbale, table de valeur, représentation visuelle et représentation algébrique).
Après le card sort, il est possible d’avoir une discussion sur les notions d’équivalence et de commutativité.
Traduction: Julie Cléroux
Ce polygraphe est conçu pour susciter des conversations riches sur les histogrammes. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: allure, centre, étendue, symétrie, incliner à droite, incliner à gauche, moyenne, médiane, extremums.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des histogrammes de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser une langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Julie Cléroux
Dans cette activité, les élèves doivent écrire des équations linéaires pour modéliser le parcours d’une balle de golf. Cette activité suppose que les élèves ont de l’expérience dans la représentation graphique d’équations linéaires.
Astuce du pro: Pour les élèves qui ont du mal à démarrer sur un trou en particulier, invitez-les à tracer un point quelque part entre la balle et le trou à utiliser comme «cible» lors de la création du premier segment de droite.
Note: Les trous 6-7 ont été créés par Christopher Kunkel. Voir l’article du blog pour plus de détails: http://whenmathhappens.com/2014/04/11/putt-putt-golf/
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves utilisent un modèle pour prédire le coût d’une pizza extra-large, basé sur des informations à propos de la taille et le coût de deux petites pizzas. Les élèves choisissent entre un modèle linéaire, quadratique ou exponentiel, ou construisent le leur avec une fonction différente s’ils le souhaitent. Les élèves interpréteront également les paramètres de leur équation en contexte.
Crédit d’image: écrans 1-4, papajohns.com
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur l’impact de (h, k) sur la forme canonique d’une équation d’une parabole. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: translation, déplacement, glissement, horizontal, vertical, sommet, axe de symétrie, axes, quadrant, valeur de x et valeur de y.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les fonctions exponentielles. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend:quadrant, intersection, asymptote.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves explorent l’idée d’ «inclinaison» de segments de droite. Cette activité sert de prélude à des conversations formelles sur le déplacement vertical, le déplacement horizontal et la pente.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves compareront les pentes des droites avec une ordonnée à l’origine de zéro. Ils utiliseront leurs comparaisons pour apprendre à écrire les équations des droites de la forme y = ax.
Inspiré par l’étude du taux de variation d’une équation de Caleb Rothe:
https://teacher.desmos.com/activitybuilder/custom/5673095054bf1351078e195d#
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les fonctions racine carrée. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: sommet, intersection, quadrant, ouverte vers le haut et ouverte vers le bas et translation.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les fonctions sinusoïdales. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: amplitude, période, maximum, minimum et translation.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les nuages de points. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: corrélation forte, corrélation faible, absence de corrélation, corrélation positive, corrélation négative, linéaire, non-linéaire, croissante et décroissante.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les fractions. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: numérateur, dénominateur, positive, négative, fraction, fraction impropre, simplifiée, équivalente, développement décimal fini, développement décimal périodique, plus près de 1 et plus près de 0.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action. Traduction: Jocelyn Dagenais
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les fonctions rationnelles. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: asymptote, verticale, horizontale, quadrant, axe, en augmentant, en diminuant, réflexion, rotation, symétrique.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour susciter des conversations riches sur les nombres rationnels et irrationnels. Le vocabulaire clé qui peut apparaître dans les questions de l’élève comprend: positif, négatif, fraction, rationnel et irrationnel.
Dans les premiers tours du jeu, les élèves peuvent remarquer des caractéristiques des nombres de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué à deux ou trois parties, pensez à prendre une courte pause pour discuter de stratégies, mettre en évidence les meilleures questions et encourager les élèves à utiliser un langage mathématique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage mathématique en action.
Traduction: Jocelyn Dagenais
Les élèves utiliseront les taux unitaires de diverses façons pour comparer la sucrosité de cinq céréales. Ils classent les céréales des moins aux plus sucrées et interprètent des graphiques pour déterminer les informations utiles, en particulier le taux unitaire.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves utilisent des fonctions sinusoïdales pour modéliser les données d’ensoleillement pour deux villes américaines (Fairbanks, Alaska et Miami, Floride). Ils prédisent quelle ville a le plus d’ensoleillement au cours d’une année donnée, puis utilisent leur modèle pour calculer une réponse à cette question. (Ils pourraient être surpris !)
Les étudiants en calcul ont ici l’occasion de pratiquer la définition et le calcul d’intégrales définies, tandis que les étudiants des cours antérieurs auront besoin de tirer parti du fait que la valeur moyenne d’une fonction sinusoïdale est égale à la droite parallèle à l’axe des x passant par le point d’inflexion.
Source de données: http://aa.usno.navy.mil/data/docs/Dur_OneYear.php
Traduction: Jocelyn Dagenais
Dans cette activité Desmos-ifiée d’un problème mathématique classique, les élèves construirons d’abord des expressions avec des nombres afin de déterminer le nombre de tuiles nécessaire pour compléter le contour d’une piscine. Ensuite ils utiliseront ces expressions numériques afin de les aider à écrire des expressions avec des VARIABLES. Pour terminer, ils testeront leur expression algébrique et voir si cela les aide à trouver le nombre de tuiles pour plusieurs piscines très rapidement.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves pratiqueront l’addition et la soustraction de nombres décimaux. Ils vont créer des expressions pour correspondre à des critères donnés (par exemple, la plus grande valeur, la plus près de zéro, etc.). Les élèves raisonnent de façon abstraite et structurée, en soutenant que leurs expressions sont les plus grandes ou les plus près de zéro possibles.
Voir des problèmes similaires à: http://openmiddle.com.
Traduction:Jocelyn Dagenais
Dans cette activité, les élèves pratiqueront l’addition et la soustraction de fractions. Ils créeront des expressions correspondant à des critères donnés (par exemple, la valeur la plus élevée, la plus petite valeur positive, etc.). Les élèves vont raisonner de façon abstraite et structurée, en argumentant que leurs expressions sont les plus grandes ou les plus petites possibles.
Voir des problèmes similaires à: http://openmiddle.com.
Traduction: Jocelyn Dagenais
Dans cette activité, les élèves rassemblent des données, construisent un modèle, puis utilisent ce modèle pour répondre à la question «Combien de pièces de 1 cent peuvent entrer dans un grand cercle?
Traduction: Jocelyn Dagenais
Les élèves utiliseront des modèles quadratiques pour optimiser la superficie d’un terrain pour un périmètre donné. C’est le traitement Desmos d’une tâche aussi ancienne que les terrain eux-mêmes. Nous mettons l’accent sur l’estimation, la construction et la formulation, en plus du graphique et de la solution que vous trouvez dans les façons de faire traditionnelles pour cette activité.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour créer des conversations riches à propos cercles et ellipses. Le vocabulaire qui pourrait apparaître dans les questions des élèves est: centre, rayon, horizontale, verticale, translation, étirement et origine.
Dans les premiers tours de la partie, les élèves peuvent remarquer les caractéristiques graphiques de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué 2-3 parties, envisagez de prendre une courte pause pour discuter de la stratégie, mettre en évidence les questions efficaces et encourager les élèves à utiliser un langage académique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage précis en action.
Traduction: Jocelyn Dagenais
Ce Polygraph est conçu pour créer des conversations riches à propos coniques. Le vocabulaire qui pourrait apparaître dans les questions des élèves est: ellipses, hyperboles, cercles et paraboles.
Dans les premiers tours de la partie, les élèves peuvent remarquer les caractéristiques graphiques de la liste ci-dessus, même s’ils ne peuvent pas utiliser ces mots pour les décrire. C’est là que vous pouvez intervenir. Après que la plupart des élèves ont joué 2-3 parties, envisagez de prendre une courte pause pour discuter de la stratégie, mettre en évidence les questions efficaces et encourager les élèves à utiliser un langage académique de plus en plus précis. Ensuite, demandez-leur de jouer plusieurs autres parties, en mettant ce langage précis en action.
Traduction: Jocelyn Dagenais